埃氏筛

1.1 简介

埃氏筛也算是一个老生常谈的算法了。给定上界 $n$ ，埃氏筛可以快速地找出 $2-n$ 之间的所有素数。

埃氏筛的想法也很简单，由小到大地遍历 $2-n$ 之间的每一个数，当我们找到一个素数 $i$ 时，可以知道 $2i、… [\frac{n}{i}]i$ 均是合数。那么当我们找到一个数 $p$ ，如果 $p$ 在这之前并没有被判断为合数，说明在 $2-p$ 之间我们并没有找到过 $p$ 的任何因子，那么 $p$ 就一定是个素数。而对于一个合数 $c$，我们在遍历到 $c$ 之前一定会先遇到 $c$ 的某一素因子，换言之我们在遍历到 $c$ 时就已经知道了 $c$ 是合数。

1.2 时间复杂度分析

对埃氏筛而言，一个比较有意思的话题是如何去估计它的时间复杂度。假设 $2-n$ 之间有 $n_p$ 个素数，则对这 $n_p$ 个素数所做的操作数是 $O(\frac{n}{n_p})$，这意味着总操作数是 $(n-n_p) * O(1) + n_p * O(n) = O(n_pn)$，而Euler给出 $n_p$ 有上界 $loglogn$，故最终的时间复杂度估计为 $O(nloglogn)$。

下面我们给出Euler关于 $n_p$ 的上界的证明。结论是

首先可以对调和级数中每个数进行素因子分解，有

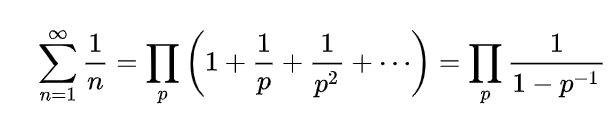
然后取对数并对 $log(1-\frac{1}{p})$ 做Taylor展开，得

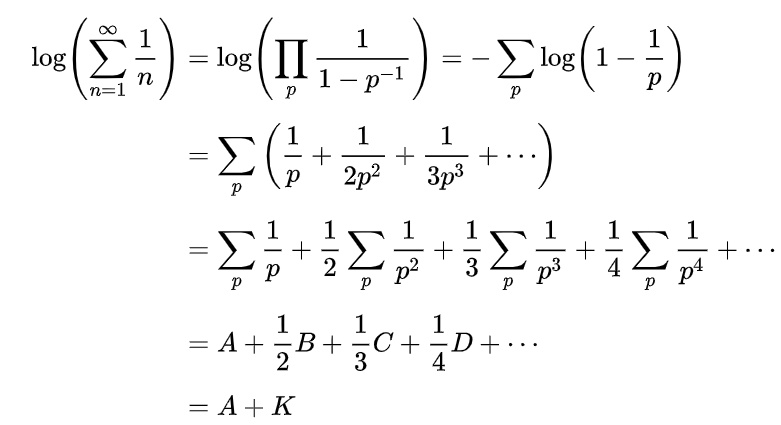
稍微做一点放缩可以证到 $K \lt 1$，例如

然后再根据Euler对调和级数求和的结论调和级数是 $logn$ 级的，就可以估出 $A$ 是 $loglogn$ 级的。因为

1.3 实现

下面给两个埃氏筛的实现。

cpp version:

# include <iostream>
# include <vector>
# include <algorithm>
using namespace std;

# define MAXN 100005

int prime[MAXN];
bool is_prime[MAXN];

int seive(int n){
    int p = 0;
    fill(prime, prime + n + 1, 0);
    fill(is_prime, is_prime + n + 1, 1);

    is_prime[0] = is_prime[1] = 0;

    for (int i = 2; i <= n; i++)
    {
        if(is_prime[i]){
            prime[p++] = i;
            for (int j = i * i; j <= n; j += i)
            {
                is_prime[j] = 0;
            }
        }
    }
    return p;
}

int main(){
    int n;
    scanf("%d",&n);
    seive(n);
    return 0;
}

注意在求解埃氏筛的时候计算 j = i*i 的一步可能会发生上溢。

py version:

def seive(n:int)->list:
    is_prime = [1]*(n+1)
    is_prime[0] = is_prime[1] = 0
    prime = []
    for i in range(2,n+1):
        if is_prime[i]:
            prime.append(i)
            for j in range(i*i, n+1, i):
                is_prime[j] = 0
    return prime


if __name__ == "__main__":
    n = int(input())
    seive(n)

追加内容：

我在上网冲浪时看到了埃氏筛的一个简单的优化。想法是在筛 $[2,n]$ 之间的素数时，我们首先只用考虑在 $[2,[\sqrt{n}]]$ 上执行埃氏筛。这时在 $[2,[\sqrt{n}]]$ 之间的素数在 $[[\sqrt{n}]+1 , n]$ 之间的倍数也会被筛去。而这时 $[[\sqrt{n}]+1 , n]$ 之间的合数已经全被筛完了。 因为 $[2,n]$ 之间的合数不可能只有 $[[\sqrt{n}]+1 , n]$ 之间的素因子。

采用这种优化后的埃氏筛代码可以写成

def sieveE(n):
    primes = [True] * (n + 1)
    primes[0] = False
    primes[1] = False
    prime_nums = []
    for i in range(2, int(n ** 0.5) + 1):
        if primes[i]:
            prime_nums.append(i)
            for j in range(i * i, n + 1 ,i):
                primes[j] = False
    return prime_nums + [i for i in range(int(n**0.5)+1, n+1)
                         if primes[i]], primes

1.4 例子

我们这里就给一个简单的例子。

AMR11E - Distinct Primes on spoj：

给定 $1 \lt n \lt 1000$，找到第 n 个 lucky number，lucky number 指至少有 3 个不同的素因子的数。

用埃氏筛显然可以估计某个区间内每个数不同的素因子个数。首先埃氏筛能找出区间内的每个素数，也能找出每个素数对应的倍数。

直接看下面的代码。

def sieve(n):
    primes = [0] * (n + 1)
    primes[0] = -1
    primes[1] = -1
    for i in range(2, n + 1):
        if not primes[i]: # 0 for prime
            for j in range(i + i, n + 1, i):
                primes[j] += 1
    return [i for i in range(2, n + 1) if primes[i] >= 3]


def solution():
    res = sieve(2700)
    T = int(input())
    for t in range(T):
        n = int(input())
        print(res[n-1])
        

if __name__ == "__main__":
    solution()

稍微比较难的一个点在于如何估计出只用筛到2700，方案是可以先筛大一点，然后取n=1000看看输出值。